Probabilistic logic
The aim of a probabilistic logic (or probability logic) is to combine the capacity of probability theory to handle uncertainty with the capacity of deductive logic to exploit structure. The result is a richer and more expressive formalism with a broad range of possible application areas. Probabilistic logic is a natural extension of traditional logic truth tables: the results they define are derived through probabilistic expressions instead. The difficulty with probabilistic logics is that they tend to multiply the computational complexities of their probabilistic and logical components.
Contents |
Proposals
There are numerous proposals for probabilistic logics:
- The term "probabilistic logic" was first used in a paper by Nils Nilsson published in 1986, where the truth values of sentences are probabilities[1]. The proposed semantical generalization induces a probabilistic logical entailment, which reduces to ordinary logical entailment when the probabilities of all sentences are either 0 or 1. This generalization applies to any logical system for which the consistency of a finite set of sentences can be established.
- In the theory of probabilistic argumentation[2][3], probabilities are not directly attached to logical sentences. Instead it is assumed that a particular subset
of the variables 
involved in the sentences defines a probability space over the corresponding sub-σ-algebra. This induces two distinct probability measures with respect to , which are called degree of support and degree of possibility, respectively. Degrees of support can be regarded as non-additive probabilities of provability, which generalizes the concepts of ordinary logical entailment (for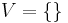 
) and classical posterior probabilities (for 
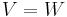). Mathematically, this view is compatible with the Dempster-Shafer theory. - The theory of evidential reasoning[4] also defines non-additive probabilities of probability (or epistemic probabilities) as a general notion for both logical entailment (provability) and probability. The idea is to augment standard propositional logic by considering an epistemic operator K that represents the state of knowledge that a rational agent has about the world. Probabilities are then defined over the resulting epistemic universe Kp of all propositional sentences p, and it is argued that this is the best information available to an analyst. From this view, Dempster-Shafer theory appears to be a generalized form of probabilistic reasoning.
- Approximate reasoning formalism proposed by fuzzy logic can be used to obtain a logic in which the models are the probability distributions and the theories are the lower envelopes[5]. In such a logic the question of the consistency of the available information is strictly related with the one of the coherence of partial probabilistic assignment and therefore with Dutch book phenomenon.
- The central concept in the theory of subjective logic[6] are opinions about some of the propositional variables involved in the given logical sentences. A binomial opinion applies to a single proposition and is represented as a 3-dimensional extension of a single probability value to express various degrees of ignorance about the truth of the proposition. For the computation of derived opinions based on a structure of argument opinions, the theory proposes respective operators for various logical connectives, such as e.g. multiplication (AND), comultiplication (OR), division (UN-AND) and co-division (UN-OR) of opinions [7] as well as conditional deduction (MP) and abduction (MT) [8].
- Markov logic networks implement a form of uncertain inference based on the maximum entropy principle -- the idea that probabilities should be assigned in such a way as to maximize entropy, in analogy with the way that Markov chains assign probabilities to finite state machine transitions.
- Probabilistic logic networks is an implementation of a probilistic logic system, using techniques and algorithms from logic programming and other systems.
Possible application areas
- Argumentation theory
- Artificial intelligence
- Bioinformatics
- Formal epistemology
- Game theory
- Philosophy of science
- Psychology
- Statistics
See also
- Statistical relational learning
- Bayesian inference, Bayesian networks, Bayesian probability
- Cox's theorem
- Dempster-Shafer theory
- Fuzzy logic
- Imprecise probability
- Logic, Deductive logic, Non-monotonic logic
- Probabilistic database
- Probability, Probability theory
- Probabilistic argumentation
- Reasoning
- Subjective logic
- Uncertainty
- Upper and lower probabilities
References
- ^ Nilsson, N. J., 1986, "Probabilistic logic," Artificial Intelligence 28(1): 71-87.
- ^ Kohlas, J., and Monney, P.A., 1995. A Mathematical Theory of Hints. An Approach to the Dempster-Shafer Theory of Evidence. Vol. 425 in Lecture Notes in Economics and Mathematical Systems. Springer Verlag.
- ^ Haenni, R, 2005, "Towards a Unifying Theory of Logical and Probabilistic Reasoning," ISIPTA'05, 4th International Symposium on Imprecise Probabilities and Their Applications: 193-202. [1]
- ^ Ruspini, E.H., Lowrance, J., and Strat, T., 1992, "Understanding evidential reasoning," International Journal of Approximate Reasoning, 6(3): 401-424.
- ^ Gerla, G., 1994, "Inferences in Probability Logic," Artificial Intelligence 70(1–2):33–52.
- ^ Jøsang, A., 2001, "A logic for uncertain probabilities," International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems 9(3):279-311.
- ^ Jøsang, A. and McAnally, D., 2004, "Multiplication and Comultiplication of Beliefs," International Journal of Approximate Reasoning, 38(1), pp.19-51, 2004
- ^ Jøsang, A., 2008, "Conditional Reasoning with Subjective Logic," Journal of Multiple-Valued Logic and Soft Computing, 15(1), pp.5-38, 2008.
Further reading
- Adams, E. W., 1998. A Primer of Probability Logic. CSLI Publications (Univ. of Chicago Press).
- Bacchus, F., 1990. "Representing and reasoning with Probabilistic Knowledge. A Logical Approach to Probabilities". The MIT Press.
- Carnap, R., 1950. Logical Foundations of Probability. University of Chicago Press.
- Chuaqui, R., 1991. Truth, Possibility and Probability: New Logical Foundations of Probability and Statistical Inference. Number 166 in Mathematics Studies. North-Holland.
- Hájek, A., 2001, "Probability, Logic, and Probability Logic," in Goble, Lou, ed., The Blackwell Guide to Philosophical Logic, Blackwell.
- Kyburg, H. E., 1970. Probability and Inductive Logic Macmillan.
- Kyburg, H. E., 1974. The Logical Foundations of Statistical Inference, Dordrecht: Reidel.
- Kyburg, H. E. & C. M. Teng, 2001. Uncertain Inference, Cambridge: Cambridge University Press.
- Romeiyn, J. W., 2005. Bayesian Inductive Logic. PhD thesis, Faculty of Philosophy, University of Groningen, Netherlands. [2]
- Williamson, J., 2002, "Probability Logic," in D. Gabbay, R. Johnson, H. J. Ohlbach, and J. Woods, eds., Handbook of the Logic of Argument and Inference: the Turn Toward the Practical. Elsevier: 397-424.